Regelmatige veelhoek
Onlangs moest ik voor een programmeeropdracht de omtrek en oppervlakte bepalen voor een regelmatige \(n\)-hoek die ingeschreven is in een cirkel met straal \(r\).
In Figuur 1 is ter illustratie een regelmatige zeshoek afgebeeld. De cirkel wordt verdeeld in \(n\) segmenten en door de hoekpunten op de cirkel met elkaar te verbinden krijg je \(n\) gelijkbenige driehoeken. Rond het middelpunt heb je dan \(n\) hoeken met sectorhoek \(\theta\). De veelhoek is een polygoon opgebouwd uit \(n\) lijnstukken (koordes), elk met lengte \(z\).
De omtrek van een regelmatige n-hoek is \(n\cdot z\) en de oppervlakte is \(n\) keer de oppervlakte van de driehoek. Voor beide berekeningen heb je de grootte van \(z\) nodig.
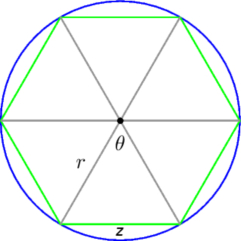
Omdat de volledige middelpuntshoek gelijk is aan \(2\pi\) radialen, is grootte van de sectorhoek
\[ \theta = \frac{2\pi}{n} \tag{1}\]
De driehoek wordt nu gedetailleerder bekeken. Via de hoogtelijn \(h\) kan deze verdeeld worden in twee gelijke rechthoekige driehoeken, zie Figuur 2.
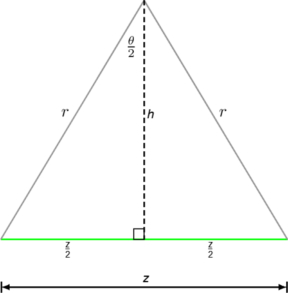
De zijde \(z\) kan berekend worden via de formule voor de sinus in een rechthoekige driehoek.
\[ sin(\frac{\theta}{2}) = \frac{z}{2r} => z = 2\cdot r\cdot sin(\frac{\theta}{2}) = 2\cdot r\cdot sin(\frac{\pi}{n}) \tag{2}\]
Dus omtrek regelmatige n-hoek is dan
\[ n\cdot z = 2\cdot n\cdot r\cdot sin(\frac{\pi}{n}) \tag{3}\]
En met de formule voor de cosinus kan de hoogte \(h\) berekend worden.
\[ cos(\frac{\theta}{2}) = \frac{h}{r} => h = r\cdot cos(\frac{\theta}{2}) = r\cdot cos(\frac{\pi}{n}) \tag{4}\]
De oppervlakte van de driehoek is
\[ \frac{z\cdot h}{2} =\frac{2 r sin(\frac{\pi}{n})\cdot r cos(\frac{\pi}{n})}{2}= r^2sin(\frac{\pi}{n})cos(\frac{\pi}{n})=\frac{1}{2}r^2 sin(\frac{2\pi}{n}) \tag{5}\]
Dus oppervlakte regelmatige n-hoek is dan
\[ \frac{1}{2}n r^2 sin(\frac{2\pi}{n}) \tag{6}\]